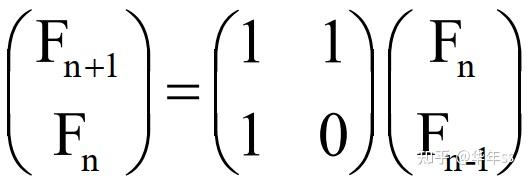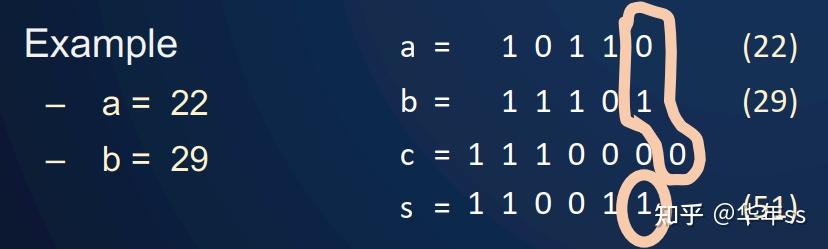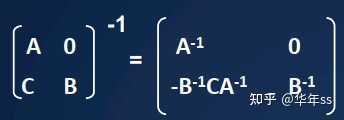尤其是模型并行,求白话解释
数据并行就是把train set分布给不同的worker,每个worker通过缓存在本地的,分配到的数据集来更新一个共有的parameter,比如mini-batch中每个worker随机从本地数据集中选出一个batch,更新parameter。 关键点在于如何管理共有的paramter,比如有经典的ps和petuum 的ssp改进。petuum的bosen就是这种数据并行方式。
模型并行我只有大体的了解。比如一个model有1000维的parameter,那么通过某种算法让10个worker中的每个只负责10维的parameter的更新。 petuum的strads是模型并行的。
最后安利下我自己的基于c++分布式平台Dogee,使用DSM模型,管理本地内存数据和管理分布式内存一样简单
http://github.com/Menooker/Dogee
很巧这个问题出现在我的推荐上,一打开知乎就看到,遂答一发。
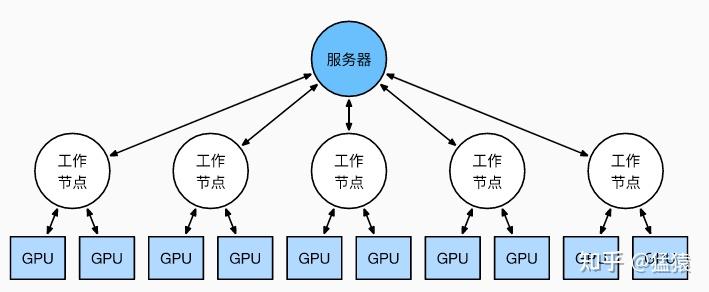
首先说下为什么要并行,众所周知目前的深度学习领域就是海量的数据加上大量的数学运算,所以计算量相当的大,训练一个模型跑上十天半个月啥的是常事。那此时分布式的意义就出现了,既然一张GPU卡跑得太慢就来两张,一台机器跑得太慢就用多台机器,于是我们先来说说数据并行,放张网上copy的图
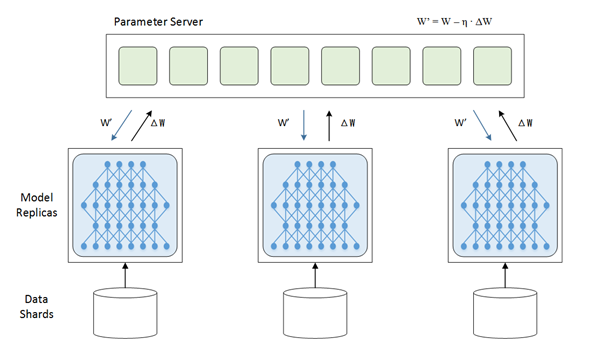
在上面的这张图里,每一个节点(或者叫进程)都有一份模型,然后各个节点取不同的数据,通常是一个batch_size,然后各自完成前向和后向的计算得到梯度,这些进行训练的进程我们成为worker,除了worker,还有参数服务器,简称ps server,这些worker会把各自计算得到的梯度送到ps server,然后由ps server来进行update操作,然后把update后的模型再传回各个节点。因为在这种并行模式中,被划分的是数据,所以这种并行方式叫数据并行。
然后呢咱们来说说模型并行,深度学习的计算其实主要是矩阵运算,而在计算时这些矩阵都是保存在内存里的,如果是用GPU卡计算的话就是放在显存里,可是有的时候矩阵会非常大,比如在CNN中如果num_classes达到千万级别,那一个FC层用到的矩阵就可能会大到显存塞不下。这个时候就不得不把这样的超大矩阵给拆了分别放到不同的卡上去做计算,从网络的角度来说就是把网络结构拆了,其实从计算的过程来说就是把矩阵做了分块处理。这里再放一张网上盗的图表示下模型并行:
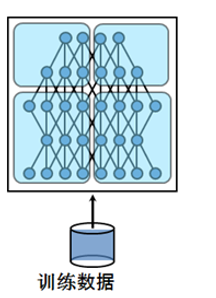
最后说说两者之间的联系,有的时候呢数据并行和模型并行会被同时用上。比如深度的卷积神经网络中卷积层计算量大,但所需参数系数 W 少,而FC层计算量小,所需参数系数 W 多。因此对于卷积层适合使用数据并行,对于全连接层适合使用模型并行。 就像这样:
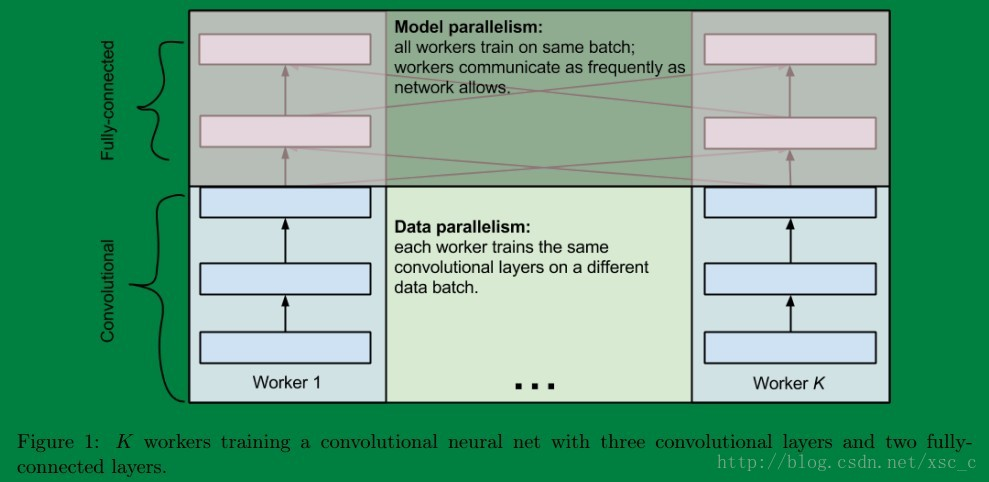
关于这个更多地可以参考这篇博客,说的挺详细的卷积神经网络的并行化模型--One weird trick for parallelizing convolutional neural networks

作者|Lilian Weng、Greg Brockman
翻译|董文文
AI领域的许多最新进展都围绕大规模神经网络展开,但训练大规模神经网络是一项艰巨的工程和研究挑战,需要协调GPU集群来执行单个同步计算。
随着集群数和模型规模的增长,机器学习从业者开发了多项技术,在多个GPU上进行并行模型训练。
乍一看,这些并行技术令人生畏,但只需对计算结构进行一些假设,这些技术就会变得清晰——在这一点上,就像数据包在网络交换机之间传递一样,那也只是从A到B传递并不透明的位(bits)。
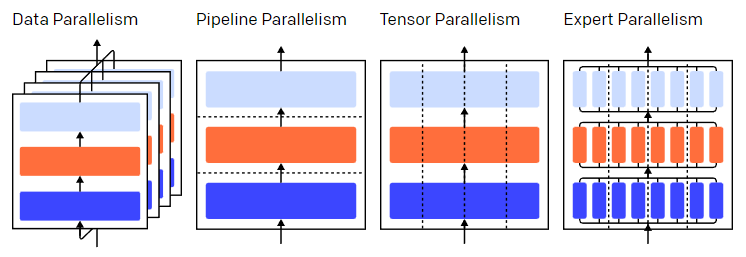 三层模型中的并行策略。每种颜色代表一层,虚线分隔不同的 GPU。
三层模型中的并行策略。每种颜色代表一层,虚线分隔不同的 GPU。训练神经网络是一个迭代的过程。在一次迭代过程中,一批数据中的训练样本通过模型的layer(层)进行前向传递,计算得到输出。然后再通过layer进行反向传递,其中,通过计算参数的梯度,可以得到各个参数对最终输出的影响程度。
批量平均梯度、参数和每个参数的优化状态会传递给优化算法,如Adam,优化算法会计算下一次迭代的参数 ( 性能更佳)并更新每个参数的优化状态。随着对数据进行多次迭代训练,训练模型会不断优化,得到更加精确的输出。
不同的并行技术将训练过程划分为不同的维度,包括:
- 数据并行(Data Parallelism)——在不同的GPU上运行同一批数据的不同子集;
- 流水并行(Pipeline Parallelism)——在不同的GPU上运行模型的不同层;
- 模型并行(Tensor Parallelism)——将单个数学运算(如矩阵乘法)拆分到不同的GPU上运行;
- 专家混合(Mixture-of-Experts)——只用模型每一层中的一小部分来处理数据。
本文以GPU训练神经网络为例,并行技术同样也适用于使用其他神经网络加速器进行训练。作者为OpenAI华裔工程师Lilian Weng和联合创始人&总裁Greg Brockman。
数据并行是指将相同的参数复制到多个GPU上,通常称为“工作节点(workers)”,并为每个GPU分配不同的数据子集同时进行处理。
数据并行需要把模型参数加载到单GPU显存里,而让多个GPU计算的代价就是需要存储参数的多个副本。话虽如此,还有一些方法可以增加GPU的RAM,例如在使用的间隙临时将参数卸载(offload)到CPU的内存上。
更新数据并行的节点对应的参数副本时,需要协调节点以确保每个节点具有相同的参数。
最简单的方法是在节点之间引入阻塞通信:(1)单独计算每个节点上的梯度;(2) 计算节点之间的平均梯度;(3) 单独计算每个节点相同的新参数。其中,步骤 (2) 是一个阻塞平均值,需要传输大量数据(与节点数乘以参数大小成正比),可能会损害训练吞吐量。
有一些异步更新方案可以消除这种开销,但是会损害学习效率;在实践中,通常会使用同步更新方法。
流水并行是指按顺序将模型切分为不同的部分至不同的GPU上运行。每个GPU上只有部分参数,因此每个部分的模型消耗GPU的显存成比例减少。
将大型模型分为若干份连续的layer很简单。但是,layer的输入和输出之间存在顺序依赖关系,因此在一个GPU等待其前一个GPU的输出作为其输入时,朴素的实现会导致出现大量空闲时间。这些空闲时间被称作“气泡”,而在这些等待的过程中,空闲的机器本可以继续进行计算。
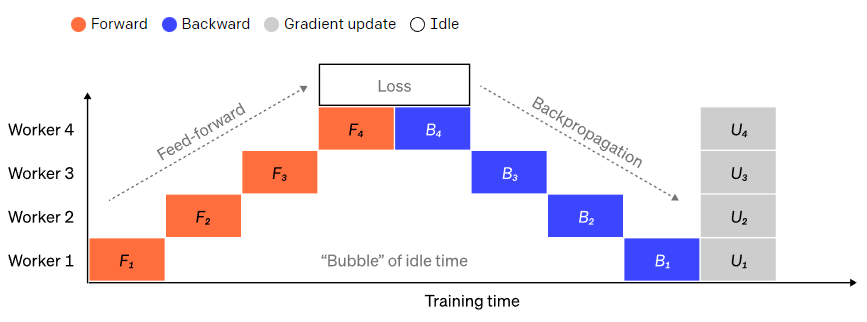 一个朴素的流水并行设置,其中模型按layer垂直分成 4 个部分。worker 1托管网络第一层(离输入最近)的模型参数,而 worker 4 托管第 4 层(离输出最近)的模型参数。“F”、“B”和“U”分别代表前向、反向和更新操作。下标指示数据在哪个节点上运行。由于顺序依赖性,数据一次只能在一个节点上运行,从而会
一个朴素的流水并行设置,其中模型按layer垂直分成 4 个部分。worker 1托管网络第一层(离输入最近)的模型参数,而 worker 4 托管第 4 层(离输出最近)的模型参数。“F”、“B”和“U”分别代表前向、反向和更新操作。下标指示数据在哪个节点上运行。由于顺序依赖性,数据一次只能在一个节点上运行,从而会
为了减少气泡的开销,在这里可以复用数据并行的打法,核心思想是将大批次数据分为若干个微批次数据(microbatches),每个节点每次只处理一个微批次数据,这样在原先等待的时间里可以进行新的计算。
每个微批次数据的处理速度会成比例地加快,每个节点在下一个小批次数据释放后就可以开始工作,从而加快流水执行。有了足够的微批次,节点大部分时间都在工作,而气泡在进程的开头和结束的时候最少。梯度是微批次数据梯度的平均值,并且只有在所有小批次完成后才会更新参数。
模型拆分的节点数通常被称为流水线深度(pipeline depth)。
在前向传递过程中,节点只需将其layer块的输出(激活)发送给下一个节点;在反向传递过程中,节点将这些激活的梯度发送给前一个节点。如何安排这些进程以及如何聚合微批次的梯度有很大的设计空间。GPipe 让每个节点连续前向和后向传递,在最后同步聚合多个微批次的梯度。PipeDream则是让每个节点交替进行前向和后向传递。
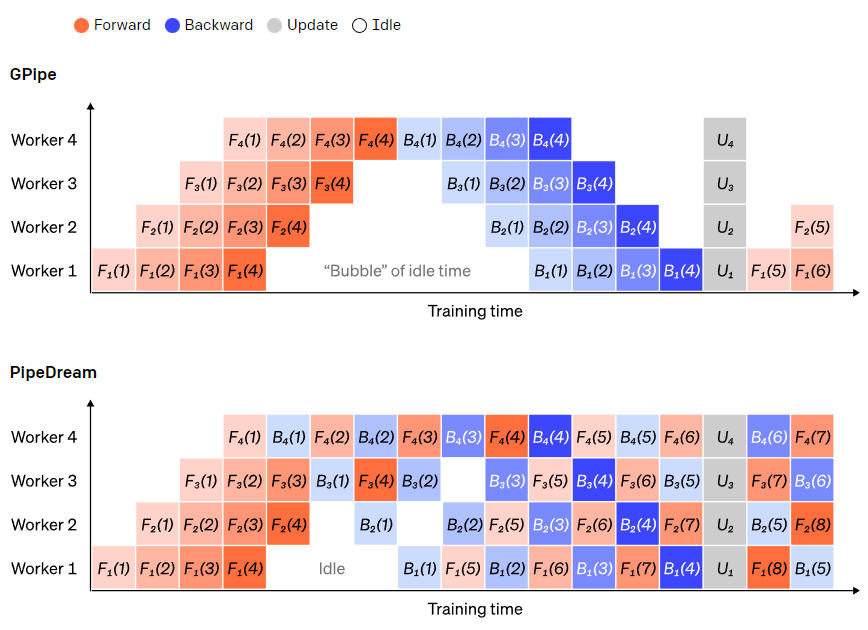 GPipe 和 PipeDream 流水方案对比。每批数据分为4个微批次,微批次1-8对应于两个连续大批次数据。图中,“(编号)”表示在哪个微批次上执行操作,下标表示节点 ID。其中,PipeDream使用相同的参数执行计算,可以获得更高的效率。
GPipe 和 PipeDream 流水方案对比。每批数据分为4个微批次,微批次1-8对应于两个连续大批次数据。图中,“(编号)”表示在哪个微批次上执行操作,下标表示节点 ID。其中,PipeDream使用相同的参数执行计算,可以获得更高的效率。
在流水并行中,模型沿layer被“垂直”拆分,如果在一个layer内“水平”拆分单个操作,这就是模型并行。许多现代模型(如 Transformer)的计算瓶颈是将激活值与权重相乘。
矩阵乘法可以看作是若干对行和列的点积:可以在不同的 GPU 上计算独立的点积,也可以在不同的 GPU 上计算每个点积的一部分,然后相加得到结果。
无论采用哪种策略,都可以将权重矩阵切分为大小均匀的“shards”,不同的GPU负责不同的部分。要得到完整矩阵的结果,需要进行通信将不同部分的结果进行整合。
Megatron-LM在Transformer的self-attention和MLP layer进行并行矩阵乘法;PTD-P同时使用模型、数据和流水并行,其中流水并行将多个不连续的layer分配到单设备上运行,以更多网络通信为代价来减少气泡开销。
在某些场景下,网络的输入可以跨维度并行,相对于交叉通信,这种方式的并行计算程度较高。如序列并行,输入序列在时间上被划分为多个子集,通过在更细粒度的子集上进行计算,峰值内存消耗可以成比例地减少。
混合专家(MoE)模型是指,对于任意输入只用一小部分网络用于计算其输出。在拥有多组权重的情况下,网络可以在推理时通过门控机制选择要使用的一组权重,这可以在不增加计算成本的情况下获得更多参数。
每组权重都被称为“专家(experts)”,理想情况是,网络能够学会为每个专家分配专门的计算任务。不同的专家可以托管在不同的GPU上,这也为扩大模型使用的GPU数量提供了一种明确的方法。
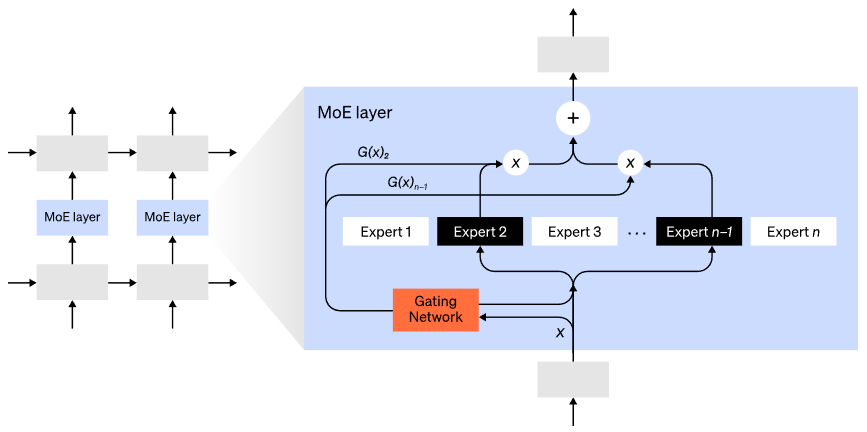 混合专家(MoE)层。门控网络只选择了n个专家中的2个(图片改编自:Shazeer et al., 2017)。
混合专家(MoE)层。门控网络只选择了n个专家中的2个(图片改编自:Shazeer et al., 2017)。GShard将MoE Transformer扩展到6000亿个参数,其中MoE layers被拆分到多个TPU上,其他layers是完全重复的。 Switch Transformer将输入只路由给一个专家,将模型大小扩展到数万亿个参数,具有更高的稀疏性。
除了以上的并行策略,还有很多其他的计算策略可以用于训练大规模神经网络:
- 要计算梯度,需要保存原始激活值,而这会消耗大量设备显存。Checkpointing(也称为激活重计算)存储激活的任何子集,并在反向传播时及时重新计算中间的激活。这可以节省大量内存,而计算成本最多就是增加一个完整的前向传递。还可以通过选择性激活重计算(https://arxiv.org/abs/2205.05198)在计算和内存成本之间不断权衡,也就是对那些存储成本相对较高但计算成本较低的激活子集进行检查。
- 混合精度训练(https://arxiv.org/abs/1710.03740)是使用较低精度的数值(通常为FP16)来训练模型。现代加速器可以用低精度的数值完成更高的FLOP计数,同时还可以节省设备显存。处理得当的话,几乎不会损失生成模型的精度。
- Offloading是将未使用的数据临时卸载到CPU或其他设备上,在需要时再将其读回。朴素实现会大幅降低训练速度,而复杂的实现会预取数据,这样设备不需要再等待数据。其中一个实现是ZeRO(https://arxiv.org/abs/1910.02054),它将参数、梯度和优化器状态分割到所有可用硬件上,并根据需要将它们实现。
- 内存效率优化器可减少优化器维护的运行状态的内存,例如Adafactor。
- 压缩可用于存储网络的中间结果。例如,Gist可以压缩为反向传递而保存的激活;DALL·E可以在同步梯度之前压缩梯度。
(原文:https://openai.com/blog/techniques-for-training-large-neural-networks/)
其他人都在看
欢迎下载体验OneFlow v0.7.0:
https://github.com/Oneflow-Inc/oneflow/
【本文是图解大模型训练2篇,持续更新中,欢迎关注】:
猛猿:图解大模型训练之:流水线并行(Pipeline Parallelism),以Gpipe为例
猛猿:图解大模型训练之:数据并行上篇(DP, DDP与ZeRO)
猛猿:图解大模型训练之:数据并行下篇(ZeRO,零冗余优化)
猛猿:图解大模型系列之:张量模型并行,Megatron-LM
猛猿:图解大模型系列之:Megatron源码解读1,分布式环境初始化
【ChatGPT算法解析系列,可见】
猛猿:ChatGPT技术解析系列之:训练框架InstructGPT(因平台bug暂时显示不出来,可以看这一篇回答
猛猿:ChatGPT技术解析系列之:GPT1、GPT2与GPT3
猛猿:ChatGPT技术解析系列之:赋予GPT写代码能力的Codex
【20231205更新】
针对评论区问得比较多的两个问题,这边做一下回复:
(1)stage1的通讯量为什么是  而不是
而不是  ?
?
先说结论:实操中是  ,按论文概念定义是
,按论文概念定义是  。
。
在实操中,我们可以只对梯度做一次scatter-reduce,并用各自维护的optimizer去更新对应的W,然后再对W做all-gather使得每块卡上都有更新后的完整W,这样通讯量就是  。
。
那么  是怎么来的呢?因为论文定义stage1只有optimizer是切开的,意味着G和W都是完整的。所以对G做all-reduce(虽然拿回完整的G并没有意义),对W做all-gather,这样通讯量就是
是怎么来的呢?因为论文定义stage1只有optimizer是切开的,意味着G和W都是完整的。所以对G做all-reduce(虽然拿回完整的G并没有意义),对W做all-gather,这样通讯量就是  。
。
本文写作时,最终选择按照论文对相关概念的定义,选择了  ,但是实操来看是完全可以用
,但是实操来看是完全可以用  实现的。评论区有朋友提到deepspeed的某次代码更新是将stage1的通讯量从
实现的。评论区有朋友提到deepspeed的某次代码更新是将stage1的通讯量从  降至
降至  ,可能也是基于此做了改进。
,可能也是基于此做了改进。
(2)stage2和stage3的流程是不是不太对?
本文在写作时,对于stage2和stage3是做了抽象的。即把整个FWD过程抽象为一个整体,把整个BWD过程抽象为一个整体,抽象过后对于一个模型就没有“layer“的概念了。这里做抽象的意义,是为了用更简明的图,来对FWD/BWD过程的通讯量做分析(可见这篇文章评论区对zlkkk这位朋友的回复)。Layer层面上Zero运作的细节,大家可以参考微软的官方博客。如果近期有时间,我也会把Layer层面的运作细节再整理下,绘制些新图po上来。
在上一篇的介绍中,我们介绍了以Google GPipe为代表的流水线并行范式。当模型太大,一块GPU放不下时,流水线并行将模型的不同层放到不同的GPU上,通过切割mini-batch实现对训练数据的流水线处理,提升GPU计算通讯比。同时通过re-materialization机制降低显存消耗。
但在实际应用中,流水线并行并不特别流行,主要原因是模型能否均匀切割,影响了整体计算效率,这就需要算法工程师做手调。因此,今天我们来介绍一种应用最广泛,最易于理解的并行范式:数据并行。
数据并行的核心思想是:在各个GPU上都拷贝一份完整模型,各自吃一份数据,算一份梯度,最后对梯度进行累加来更新整体模型。理念不复杂,但到了大模型场景,巨大的存储和GPU间的通讯量,就是系统设计要考虑的重点了。在本文中,我们将递进介绍三种主流数据并行的实现方式:
- DP(Data Parallelism):最早的数据并行模式,一般采用参数服务器(Parameters Server)这一编程框架。实际中多用于单机多卡
- DDP(Distributed Data Parallelism):分布式数据并行,采用Ring AllReduce的通讯方式,实际中多用于多机场景
- ZeRO:零冗余优化器。由微软推出并应用于其DeepSpeed框架中。严格来讲ZeRO采用数据并行+张量并行的方式,旨在降低存储。
本文将首先介绍DP和DDP,在下一篇文章里,介绍ZeRO。全文内容如下:
1、数据并行(DP)
2、分布式数据并行(DDP)
- 2.1 图解Ring-AllReduce
- 2.2 DP与DDP通讯分析
本文是大模型训练系列的第二篇,持续更新中,推荐阅读:
猛猿:图解大模型训练之:流水线并行(Pipeline Parallelism),以Gpipe为例

一个经典数据并行的过程如下:
- 若干块计算GPU,如图中GPU0~GPU2;1块梯度收集GPU,如图中AllReduce操作所在GPU。
- 在每块计算GPU上都拷贝一份完整的模型参数。
- 把一份数据X(例如一个batch)均匀分给不同的计算GPU。
- 每块计算GPU做一轮FWD和BWD后,算得一份梯度G。
- 每块计算GPU将自己的梯度push给梯度收集GPU,做聚合操作。这里的聚合操作一般指梯度累加。当然也支持用户自定义。
- 梯度收集GPU聚合完毕后,计算GPU从它那pull下完整的梯度结果,用于更新模型参数W。更新完毕后,计算GPU上的模型参数依然保持一致。
- 聚合再下发梯度的操作,称为AllReduce。
前文说过,实现DP的一种经典编程框架叫“参数服务器”,在这个框架里,计算GPU称为Worker,梯度聚合GPU称为Server。在实际应用中,为了尽量减少通讯量,一般可选择一个Worker同时作为Server。比如可把梯度全发到GPU0上做聚合。需要再额外说明几点:
- 1个Worker或者Server下可以不止1块GPU。
- Server可以只做梯度聚合,也可以梯度聚合+全量参数更新一起做
在参数服务器的语言体系下,DP的过程又可以被描述下图:
DP的框架理解起来不难,但实战中确有两个主要问题:
- 存储开销大。每块GPU上都存了一份完整的模型,造成冗余。关于这一点的优化,我们将在后文ZeRO部分做讲解。
- 通讯开销大。Server需要和每一个Worker进行梯度传输。当Server和Worker不在一台机器上时,Server的带宽将会成为整个系统的计算效率瓶颈。
我们对通讯开销再做详细说明。如果将传输比作一条马路,带宽就是马路的宽度,它决定每次并排行驶的数据量。例如带宽是100G/s,但每秒却推给Server 1000G的数据,消化肯定需要时间。那么当Server在搬运数据,计算梯度的时候,Worker们在干嘛呢?当然是在:

人类老板不愿意了:“打工系统里不允许有串行存在的任务!”,于是梯度异步更新这一管理层略诞生了。

上图刻画了在梯度异步更新的场景下,某个Worker的计算顺序为:
- 在第10轮计算中,该Worker正常计算梯度,并向Server发送push&pull梯度请求。
- 但是,该Worker并不会实际等到把聚合梯度拿回来,更新完参数W后再做计算。而是直接拿旧的W,吃新的数据,继续第11轮的计算。这样就保证在通讯的时间里,Worker也在马不停蹄做计算,提升计算通讯比。
- 当然,异步也不能太过份。只计算梯度,不更新权重,那模型就无法收敛。图中刻画的是延迟为1的异步更新,也就是在开始第12轮对的计算时,必须保证W已经用第10、11轮的梯度做完2次更新了。
参数服务器的框架下,延迟的步数也可以由用户自己决定,下图分别刻划了几种延迟情况:
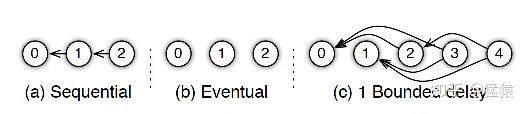
- (a) 无延迟
- (b) 延迟但不指定延迟步数。也即在迭代2时,用的可能是老权重,也可能是新权重,听天由命。
- (c) 延迟且指定延迟步数为1。例如做迭代3时,可以不拿回迭代2的梯度,但必须保证迭代0、1的梯度都已拿回且用于参数更新。
总结一下,异步很香,但对一个Worker来说,只是等于W不变,batch的数量增加了而已,在SGD下,会减慢模型的整体收敛速度。异步的整体思想是,比起让Worker闲着,倒不如让它多吃点数据,虽然反馈延迟了,但只要它在干活在学习就行。
batch就像活,异步就像画出去的饼,且往往不指定延迟步数,每个Worker干越来越多的活,但模型却没收敛取效,这又是刺伤了哪些打工仔们的心(狗头
受通讯负载不均的影响,DP一般用于单机多卡场景。因此,DDP作为一种更通用的解决方案出现了,既能多机,也能单机。DDP首先要解决的就是通讯问题:将Server上的通讯压力均衡转到各个Worker上。实现这一点后,可以进一步去Server,留Worker。
前文我们说过,聚合梯度 + 下发梯度这一轮操作,称为AllReduce。接下来我们介绍目前最通用的AllReduce方法:Ring-AllReduce。它由百度最先提出,非常有效地解决了数据并行中通讯负载不均的问题,使得DDP得以实现。
如下图,假设有4块GPU,每块GPU上的数据也对应被切成4份。AllReduce的最终目标,就是让每块GPU上的数据都变成箭头右边汇总的样子。
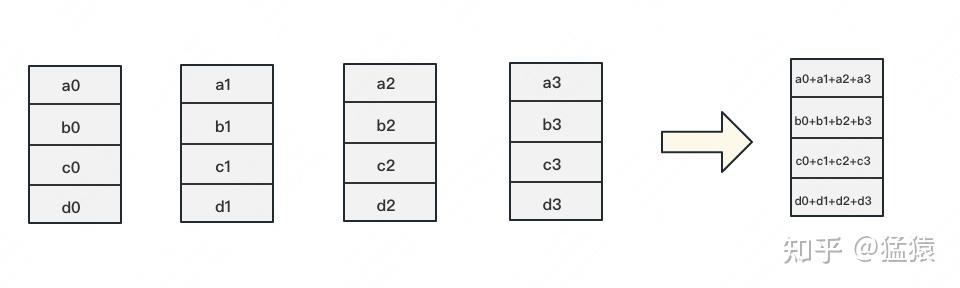
Ring-ALLReduce则分两大步骤实现该目标:Reduce-Scatter和All-Gather。
Reduce-Scatter
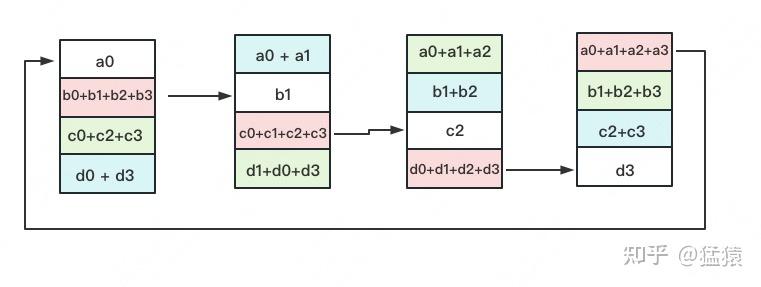
定义网络拓扑关系,使得每个GPU只和其相邻的两块GPU通讯。每次发送对应位置的数据进行累加。每一次累加更新都形成一个拓扑环,因此被称为Ring。看到这觉得困惑不要紧,我们用图例把详细步骤画出来。
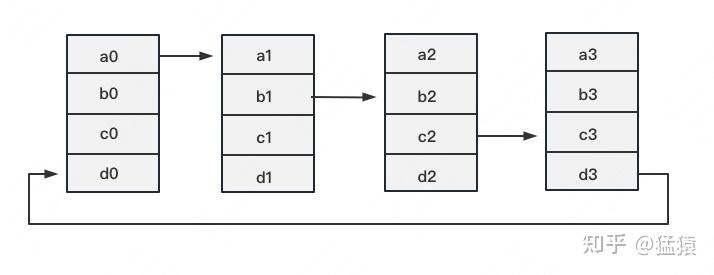
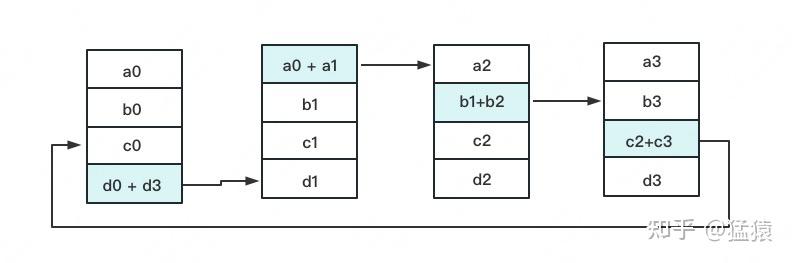
一次累加完毕后,蓝色位置的数据块被更新,被更新的数据块将成为下一次更新的起点,继续做累加操作。
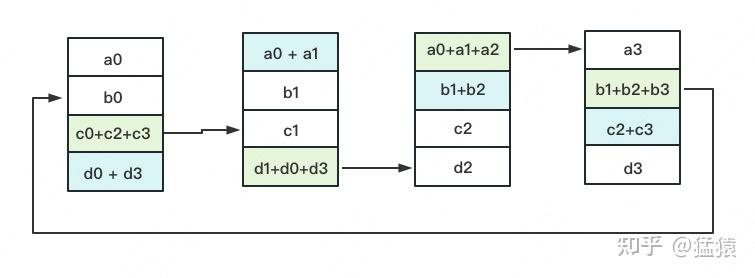

3次更新之后,每块GPU上都有一块数据拥有了对应位置完整的聚合(图中红色)。此时,Reduce-Scatter阶段结束。进入All-Gather阶段。目标是把红色块的数据广播到其余GPU对应的位置上。
All-Gather
如名字里Gather所述的一样,这操作里依然按照“相邻GPU对应位置进行通讯”的原则,但对应位置数据不再做相加,而是直接替换。All-Gather以红色块作为起点。
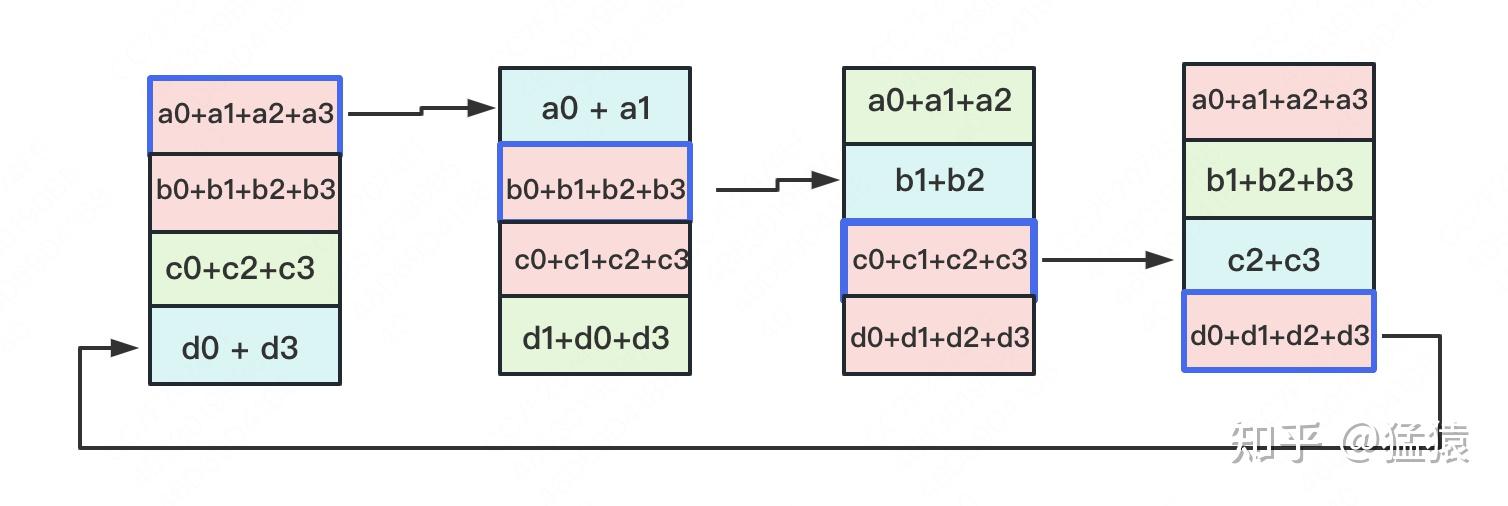
以此类推,同样经过3轮迭代后,使得每块GPU上都汇总到了完整的数据,变成如下形式:
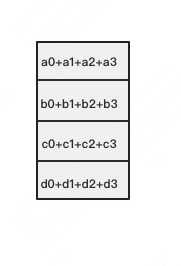
建议读者们手动推一次,加深理解。
假设模型参数W的大小为  ,GPU个数为
,GPU个数为  。则梯度大小也为
。则梯度大小也为  ,每个梯度块的大小为
,每个梯度块的大小为 
对单卡GPU来说(只算其send通讯量):
- Reduce-Scatter阶段,通讯量为

- All-Gather阶段,通讯量为

单卡总通讯量为  ,随着N的增大,可以近似为
,随着N的增大,可以近似为  。全卡总通讯量为
。全卡总通讯量为 
而对前文的DP来说,它的Server承载的通讯量是  ,Workers为
,Workers为  ,全卡总通讯量依然为
,全卡总通讯量依然为  。虽然通讯量相同,但搬运相同数据量的时间却不一定相同。DDP把通讯量均衡负载到了每一时刻的每个Worker上,而DP仅让Server做勤劳的搬运工。当越来越多的GPU分布在距离较远的机器上时,DP的通讯时间是会增加的。
。虽然通讯量相同,但搬运相同数据量的时间却不一定相同。DDP把通讯量均衡负载到了每一时刻的每个Worker上,而DP仅让Server做勤劳的搬运工。当越来越多的GPU分布在距离较远的机器上时,DP的通讯时间是会增加的。
但这并不说明参数服务器不能打(有很多文章将参数服务器当作old dinosaur来看)。事实上,参数服务器也提供了多Server方法,如下图:
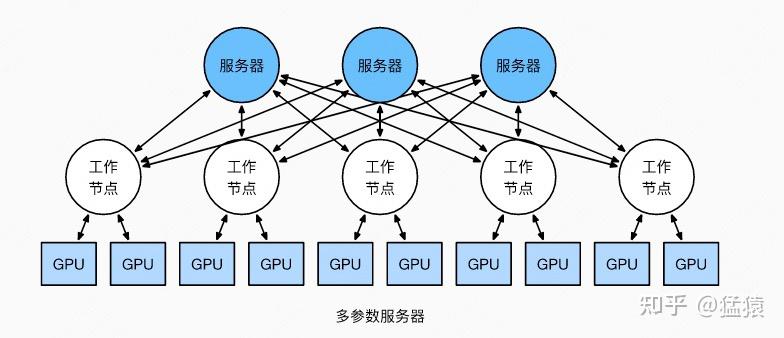
在多Server的模式下,进一步,每个Server可以只负责维护和更新某一块梯度(也可以某块梯度+参数一起维护),此时虽然每个Server仍然需要和所有Worker通讯,但它的带宽压力会小非常多。经过调整设计后,依然可以用来做DDP。虽然这篇文章是用递进式的方式来介绍两者,但不代表两者间一定要决出优劣。我想表达的观点是,方法是多样性的。对参数服务器有兴趣的朋友,可以阅读参考的第1个链接。
最后,请大家记住Ring-AllReduce的方法,因为在之后的ZeRO,Megatron-LM中,它将频繁地出现,是分布式训练系统中重要的算子。
1、在DP中,每个GPU上都拷贝一份完整的模型,每个GPU上处理batch的一部分数据,所有GPU算出来的梯度进行累加后,再传回各GPU用于更新参数
2、DP多采用参数服务器这一编程框架,一般由若个计算Worker和1个梯度聚合Server组成。Server与每个Worker通讯,Worker间并不通讯。因此Server承担了系统所有的通讯压力。基于此DP常用于单机多卡场景。
3、异步梯度更新是提升计算通讯比的一种方法,延迟更新的步数大小决定了模型的收敛速度。
4、Ring-AllReduce通过定义网络环拓扑的方式,将通讯压力均衡地分到每个GPU上,使得跨机器的数据并行(DDP)得以高效实现。
5、DP和DDP的总通讯量相同,但因负载不均的原因,DP需要耗费更多的时间搬运数据
1、https://web.eecs.umich.edu/~mosharaf/Readings/Parameter-Server.pdf
2、https://zh.d2l.ai/chapter_computational-performance/parameterserver.html
3、https://blog.csdn.net/dpppBR/article/details/80445569
4、https://arxiv.org/abs/1910.02054
5、https://blog.51cto.com/u_14691718/5631471
- 本课程来自加州伯克利大学2022年春季课程 UCB CS267并行计算机应用。主讲人为Ayd?n Bulu? 和 Jim Demmel。课程地址包括视频与幻灯片。
- 本文将收录于以下专栏
UCB CS267 并行计算机应用
凸优化、机器学习、深度学习、CUDA编程内容地址合集
- 本文为第八讲 数据并行算法,内容包括
- 数据并行
- 理想硬件与性能模型
- 数据并行的应用
- 实现数据并行的硬件
- 总结
- 上一讲中讲述了GPU编程模型,这一讲讲述数据并行算法,这种思想不仅可以用在GPU编程中,也更加一般化。
- 再次回顾本课程中涉及到的几种并行编程的硬件抽象模型:有以下三种
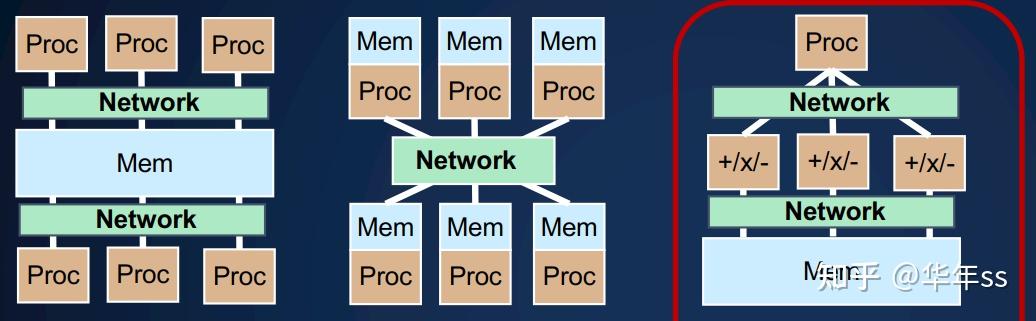
- 共享内存:每个处理器执行自己的指令流;通过读写内存实现通信;
- 分布式内存:每个处理器执行自己的指令流;通过发送消息进行通信;(下一讲的内容)
- 单指令多数据SIMD:所有处理器执行相同的指令;通过内存通信。
- 数据并行:意思是在多个值(通常是数据元素)上执行相同操作,也包括缩减reductions, 广播broadcast,扫描scan等操作。一些并行编程模型使用了一些数据并行,包括SIMD、GPU/CUDA、MapReduce、MPI集合(collective)
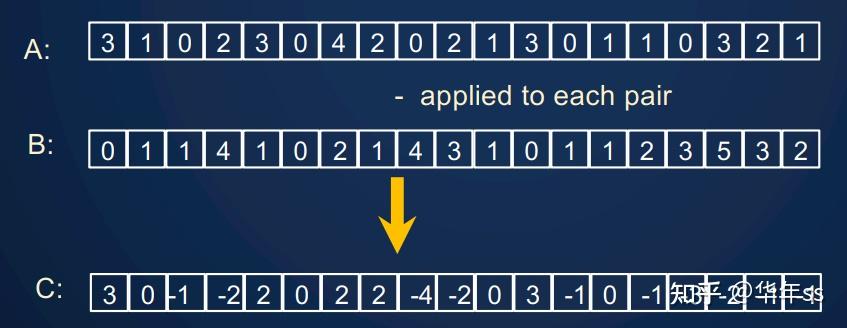
- 单一操作:例如
 是两个数组,
是两个数组, 为一元函数。执行
为一元函数。执行 。
。 - 类似的也有二元操作,即两个数组相减。
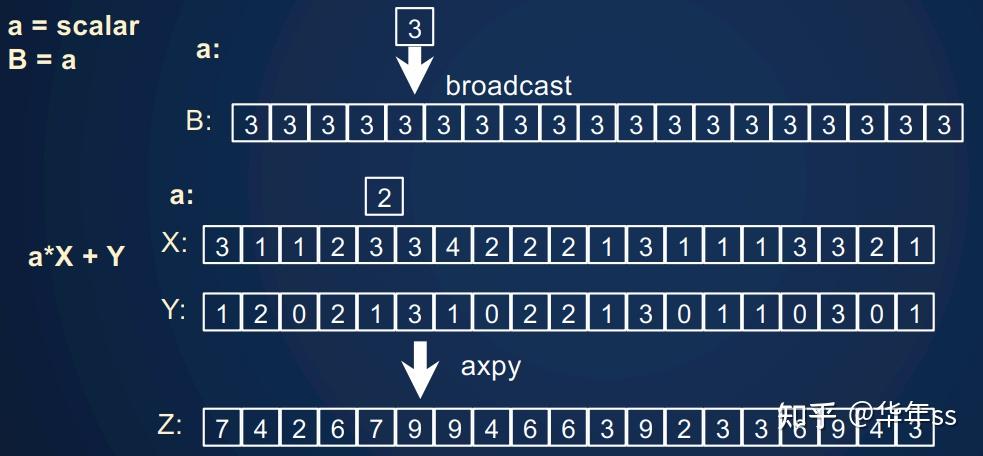
- 更复杂一些的广播(broadcast)操作。Python中也有这个概念,计算
 ,此时一个标量数与数组相乘,则会先将标量扩充维度到与数组相同,再进行后续操作。这种操作被称为axpy。
,此时一个标量数与数组相乘,则会先将标量扩充维度到与数组相同,再进行后续操作。这种操作被称为axpy。
数据可以连续地址空间复制
A: double [0:4]
B: double [0:4] = [0.0, 1.0, 2.2, 3.3, 4.4]
A = B
也可以跳步(stride)赋值(内存上不连续)
A = B [0:4:2] // 以间隔2的方式访问B中元素
C: double [0:4, 0:4]
A = C [*,3] // 复制C的列
收集(gather) :以索引的方式获取某数组中的元素
X: int [0:4] = [3, 0, 4, 2, 1] // 打乱索引顺序
A = B[X] // A 为[3.3, 0.0, 4.4, 2.2, 1.1]
散射(satter):以索引的方式获取某数组中的元素,现在索引放在等号左侧
A[X] = B // A 为[1.1, 4.4, 3.3, 0.0, 2.2]
// 如果X=[0,0,0,0,0]则可能会有写入冲突

- 缩减(reduce):将数组通过某些计算变为一个标量的操作,例如求和、平均数、向量内积等。
- 扫描(scan):逐元素累计的某种计算。例如累计求和、取最大等。下图为累计求和

scan分为inclusive和exclusive两种。inclusive在计算时,不包含当前位置;exclusive在计算时包含当前位置。例如累计加法add_scan_inclusive([1, 0, 3, 0, 2]) à[1, 1, 4, 4, 6],add_scan_exclusive([1, 0, 3, 0, 2]) à[0, 1, 1, 4, 4]。两者的结果可以通过加减原数据互相转化。
- 单指令多数据SIMD机器:
- 一个“控制处理器”分发指令
- 每个处理器执行相同的指令
- 一些处理器对于一些指令可能关闭
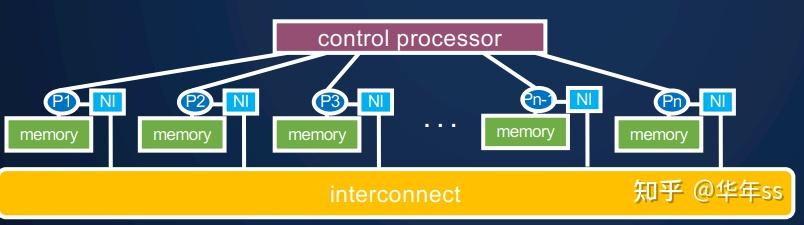
- 理想的运行成本。在理想情况下,假设处理器数量无上限为p,不考虑控制分发指令的耗费时间,不考虑通信交流成本。这种模型的成本(复杂度)由算法扫描(scan)或深度(depth)决定。
- 一元或二元操作复杂度为
 ,因为处理器数量无上限,且无需考虑通信成本;
,因为处理器数量无上限,且无需考虑通信成本; - 缩减与广播:使用树结构计算,则复杂度为
 ,且对于二分支的树结构,复杂度
,且对于二分支的树结构,复杂度 即是下限。
即是下限。

- 直接使用
 个处理器,
个处理器,
- 第一步,对于矩阵乘法中的行列相乘分别进行计算,复杂度为
 ,因为使用了
,因为使用了 个处理器;
个处理器;
- 第二步,对于行列相乘后的相加,使用
 个树结构进行计算,(结果中每个元素对应一个树)。
个树结构进行计算,(结果中每个元素对应一个树)。
- 下图中立方体的每个元素都使用一个线程进行计算。(本讲后续还会使用这个计算模型)
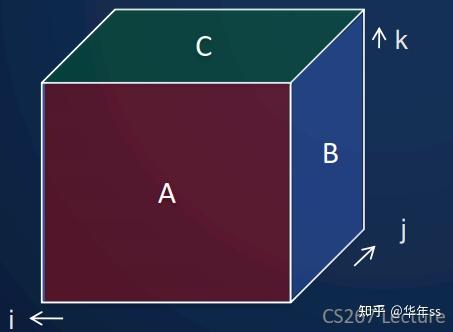
- 前面说到过的扫描计算,常为二元关系运算,比如
- 元素累计地相加,相乘,取最小,取最大;
- 布尔型运算:或,与;
- 矩阵运算:矩阵乘法
- 这种累计计算看上去就是只能串行的计算,例如
y(0) = 0;
for i = 1:n
y(i) = y(i-1) + x(i);
计算第n个值,就需要n-1次操作,且依赖于第n-1个值。看上去无法并行计算。
- 首先给出一种简便的并行方法,效率不高。
- 对于输出的每个元素都分别使用树结构计算,则计算最后一个输出结果(也是最高的)的复杂度为
 。
。 - 这么做会有很多重复计算,总的计算次数量级约为

- 下面展示另外一种计算方式。比如在计算如下结果时,后四个结果(15,21,28,36)中都需要计算(5,6,7,8)的和,那么这个和的值就可以重复使用。再进一步地1+2+3+4,1+2,3+4都可以重复使用。

? 基于上述思想,有这样一种计算scan累加的方式,步骤为:1. 成对数据求和,2.递归scan累加,3. 成对数据求和。每一步对应如下计算结果的一行。

? 总计求和计算量的递推公式为 ,易知通项公式为
,易知通项公式为 。如果使用无穷多个处理器,则时间复杂度为
。如果使用无穷多个处理器,则时间复杂度为
- 还有如下一种计算方式:看图顺序为从中间向上,再从中间向下,按照箭头方向。这种计算方式高效且节省空间(可以原位操作)。
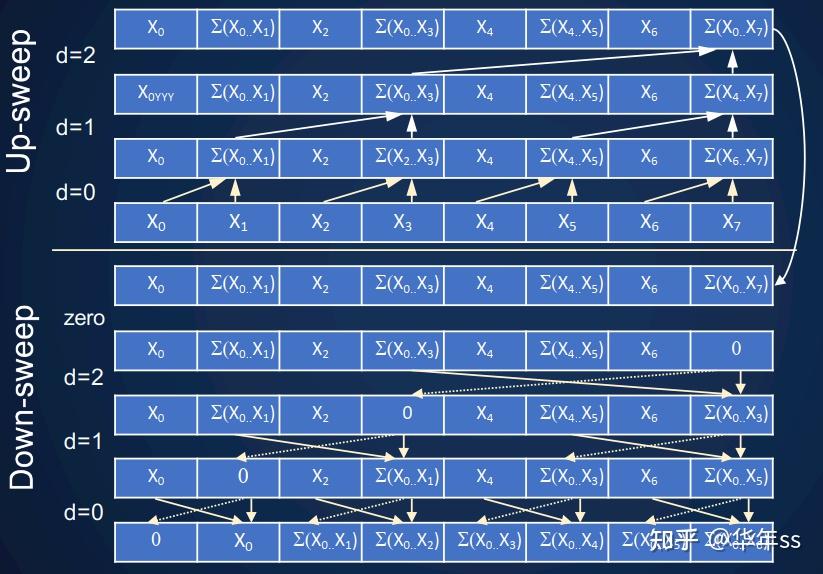
- 下面介绍一些基于扫描(scan)的应用。将上述方法用在更高级的算法中,期望在
 时间内计算完成。可以应用的场景有:
时间内计算完成。可以应用的场景有: - 在
 时间内计算两个
时间内计算两个 位整数加法;
位整数加法; - 在
 时间内计算
时间内计算 下三角矩阵的逆;
下三角矩阵的逆; - 在
 时间内计算
时间内计算 稠密矩阵的逆;
稠密矩阵的逆; - 在
 时间内对任意表达式进行评估;
时间内对任意表达式进行评估; - 在
 时间内评估递归值;
时间内评估递归值; - ”二维并行前缀“用于图像分割(Catanzaro & Keutzer);
- 稀疏矩阵-向量乘法(SpMV)使用分段扫描;
- 浏览器并行页面布局(Leo Meyerovich、Ras Bodik);
- 在
 时间内求解n乘n的三对角矩阵;
时间内求解n乘n的三对角矩阵; - 遍历链接列表;
- 计算最小生成树;
- 计算点集构成的凸包。
- 示例:压缩任务为:给定数据序列 3,2,4,1...,以及要保留的位置置1,要删除的位置置0。

- 此时计算步骤为:
- 1 对标志位(flag)计算exclusive加和扫描;
- 2 scatter赋值

- 示例:移出数组中不能被3整除的数字
int find (int x, int y) (y % x==0) ? 1 : 0;
? 取余数,后使用上面压缩数组的方式即可实现。

- 这是一种比较复杂的排序方法,先讲述串行排序方法。
- 思想:数据为二进制数,同一时间只对某位进行排序,该位是0则放在左边,该位是1则放在右边。
- 示例:排序方法如下图,前两行排最低位,奇数末尾为1较大先放到后面,偶数末位为0,排在前面;再排次低位,X0X<X1X;再排最高位,0XX<1XX。
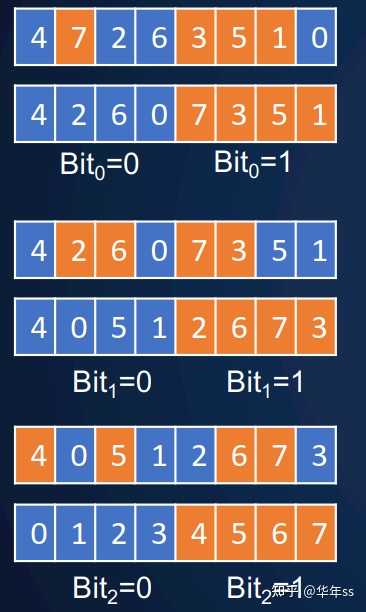
- 实际执行这个排序算法时,单步排序要用到的步骤包括:
- 获取最后一位为奇数的序号,odds;
- 获取最后一位为偶数的序号(与上一行互补),evens;
- 对上一行偶数位做exclusive 扫描求和,evpos;
- 对偶数总数做广播,扩充到与原序列等长totalEvens;
- 生成顺序索引indx=[0,1,2,3,...];
- 计算奇数位位置oddpos=totalEvens + indx– evpos ;
- 计算新的位置pos,如果该位是偶数,则值为evpos,如果该位是奇数,则值为oddpos;
- 使用pos作为索引,对原数据进行scatter收集;
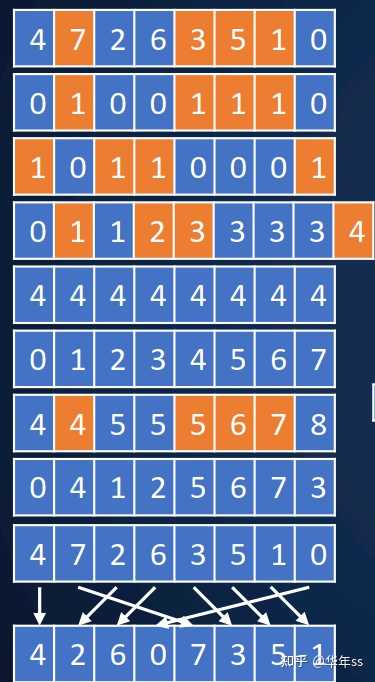
d(n)=
0 if n.next is null
1+d(n.next) otherwise
- 并行的方式大致为使用邻居的指针当做自己的指针,通过指向更远的后方,来查看自己后面还有多少元素。
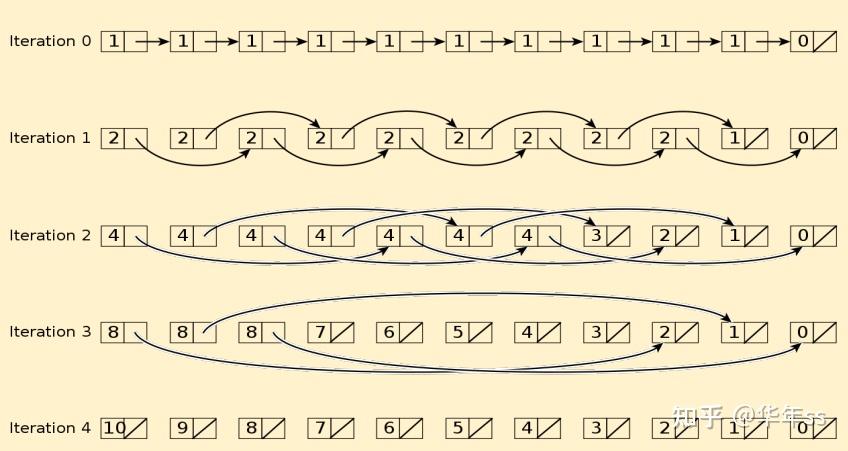

- 以上递归形式可以写为矩阵相乘
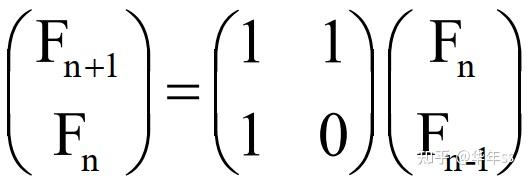
? 为了计算通项值,要累计相乘以下矩阵(可并行完成)。再与初始两个值相乘即得到结果。

- 这种思想适用于任意的线性迭代式,比如要计算

- 假设2个n位二进制数a=a[n-1]a[n-2]…a[0]和 b=b[n-1]b[n-2]…b[0],计算它们的和s=a+b=s[n]s[n-1]…s[0],c=c[n-1]…c[0]c[-1]为可能的进位。顺序循环每个位计算方式为
c[-1] = 0 //个位数之前没有进位,设置为0
for i = 0 to n-1 //从低位计算到高位
s[i] = ( a[i] xor b[i] ) xor c[i-1] //两数+进位 使用三个数的异或获得结果
c[i] = ( (a[i] xor b[i]) and c[i-1] ) or ( a[i] and b[i] ) //获得下一个进位。两数中有一个为1,且来自上一位的进位为1;或者两数都为1,才会有新的进位为1
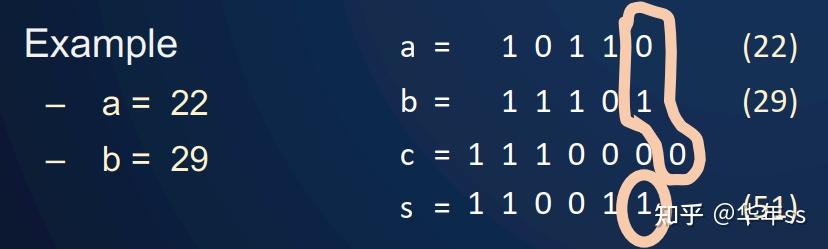
- 各位并行计算时,只是进位无法直接并行。下面讲述一种方法在
 时间内使用并行前缀(prefix)计算出进位
时间内使用并行前缀(prefix)计算出进位![c[i]](https://www.zhihu.com/equation?tex=c%5Bi%5D)
并行计算出每个位上的传播位(propagate bit)p[i]=a[i]xor b[i],生成位(generate bit)g[i]=a[i]and b[i]
? 将进位![c[i]](https://www.zhihu.com/equation?tex=c%5Bi%5D) 写为递归形式
写为递归形式

? 则M矩阵可以使用并行前缀方法计算。这种加法被称为carry look-ahead addition
- 此处指的是编译器对于代码的分析,要判断一行代码中,每个位置是关键词、字符串、关系运算符等。这个过程通过有限状态机完成。编程语言可能包括
- 标识符(Z):字符串
- 字符串(S):双引号内
- 操作符(*):+,-、=,<等
- 表达式(E),引号(Q)
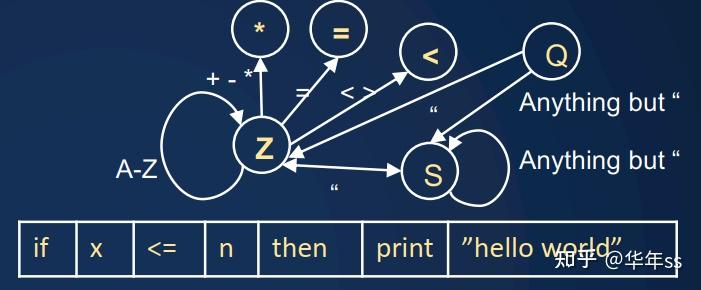
? 状态转换可以查表完成

- 这里的加速方法,大概意思是跳两个状态视为一步,也是使用并行前缀(具体没听懂)。可参考Hillis and Steele, CACM 1986
- 在
 时间内计算
时间内计算 下三角矩阵的逆;
下三角矩阵的逆;
- 下三角矩阵的逆为
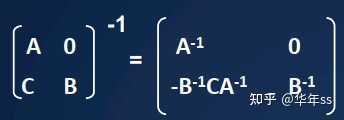
//定义函数
Tri_Inv(T)//简便起见,假设n为2的m次方
if T is 1-by-1 //如果维度为[1,1],则直接返回倒数
return 1/T
else
T=[[A,0],[C,B]] //矩阵分块,后递归调用
in parallel do {
invA = Tri_Inv( )
invB = Tri_Inv( ) // 隐含树结构
}
newC = -invB * C * invA // 矩阵乘法 log(n) 复杂度
return [[invA,0],[newC invB]]
- 上述递归算法复杂度递推公式为
time(Tri_Inv(n))=time(Tri_Inv(n/2)) + O(log(n))
- 根据递推公式可知,通项
time(Tri_Inv(n)) 复杂度为
- 在
 时间内计算
时间内计算 稠密矩阵的逆。这里使用了3条引理:
稠密矩阵的逆。这里使用了3条引理:
- 引理1:Cayley-Hamilton 定理---将
 表示为
表示为 的特征多项式形式
的特征多项式形式 - 引理2:牛顿恒等式---特征多项式系数的三角方程组,矩阵元素为

- 引理3:
![s_k=\ ext{trace}(\\mathbf{A}^k)=\\sum\\limits_{i=1}^n \\mathbf{A}^k[i,i]](https://www.zhihu.com/equation?tex=s_k%3D%5Ctext%7Btrace%7D%28%5Cmathbf%7BA%7D%5Ek%29%3D%5Csum%5Climits_%7Bi%3D1%7D%5En+%5Cmathbf%7BA%7D%5Ek%5Bi%2Ci%5D)
- 完整的算法源于Csanky (1976) ,步骤为
- 使用并行前缀计算多项式幂次
 。复杂度为
。复杂度为
- 计算迹
 。复杂度为
。复杂度为
- 解牛顿恒等式得到系数。复杂度为
 (上一点的结论)
(上一点的结论) - 使用Cayley-Hamilton 定理得到矩阵的逆。复杂度为

- 与上面说的扫描一样,但是额外附带重置位。遇到重置位,则重新开始累计。如下图累计求和,遇到标志位(第二行)为1,则从0开始累计求和。

- 早起的硬件为连接机器(Connection Machine)。早期被设计用于处理AI、机器学习计算Hillis and Handler
- CM-1,CM-2 SIMD设计
- 65536 个1位处理器,每个处理器有4KB内存
- 12维布尔 n-立方网络 (Feynman)
- CM-2添加了浮点数处理器
- 编程语言使用Lisp,C
- CM-5为RISC+向量

- 单指令多数据对于向量加法的处理。如果向量太长,硬件会自动切分为小块,然后并行地处理。
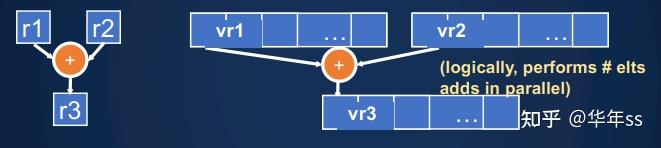
- 上节课中讲的GPU。使用大量线程并行处理,并且将线程分到线程块内。
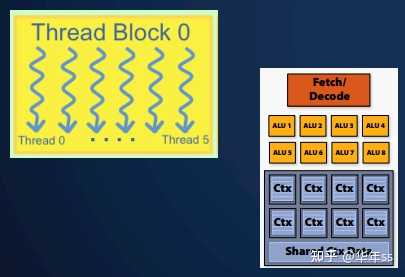
- 对于上节课GPU内容中与此相关的小结
- 分支结构是比较浪费资源的。条件判断可转为掩膜;
- 有时需要补充0或者空值,使得数据为相同长度;
- 可进行非连续地内存访问,但是更加耗费资源;
- 需要设置足够多的并行性以使得计算单元充分利用,借此掩盖内存延迟。还要做好内存/调度之间的权衡
- Massively Parallel Processing,MPP常为分布式内存,此时不仅要考虑使用多个处理器并行加速,还要考虑通信成本(这是下一节课的内容)。在分布式机器上进行缩减与广播,成本为
 。当
。当 足够大时,树结构引入的复杂度可以忽略。
足够大时,树结构引入的复杂度可以忽略。
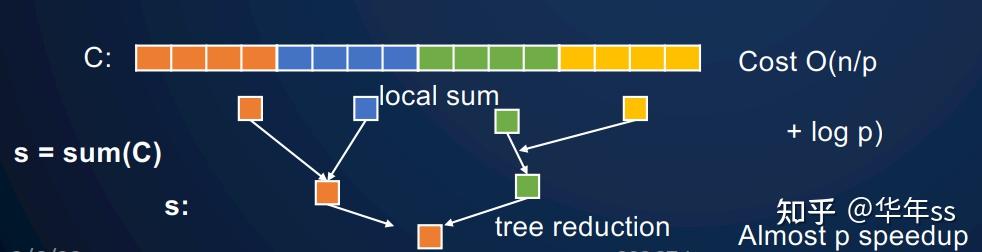
 个大型处理器上使用并行前缀的成本。
个大型处理器上使用并行前缀的成本。
- 局部单个处理器计算前缀加法用
 步;
步; - 跨所有处理器更新,用
 步
步 - 总计时间复杂度为

 复杂度并不是并行前缀有用的主要原因。假设序列长度为
复杂度并不是并行前缀有用的主要原因。假设序列长度为 每个处理器计算
每个处理器计算 百万个元素,此时成本为cost=
百万个元素,此时成本为cost= 次加法+
次加法+ 步并行扫描+
步并行扫描+ 次加法
次加法
- 串行的顺序逻辑易于调试,改正代码;
- 本节课很多复杂度分析与处理器数量无关,实际是有关的;
- 当
 时,很难进行并行映射,尤其是有嵌套结构时,内存使用也要注意;
时,很难进行并行映射,尤其是有嵌套结构时,内存使用也要注意; - 更多阅读Hillis and Steele “Data Parallel Algorithms” 和 Blelloch 的 NESL 语言与“NESL Revisited”, 2006
推荐阅读
凸优化、机器学习、深度学习、CUDA编程内容地址合集